Several weeks ago, my paper on a novel square equal-area map projection was published in ACM Transactions on Spatial Algorithms and Systems, titled A Square Equal-Area Map Projection with Low Angular Distortion, Minimal Cusps, and Closed-Form Solutions. For mathematical details, the reader is directed to the paper, but I’ll discuss what motivated its development and outline the projection’s benefits here. The projection uses a quincuncial arrangement, which places the north pole at the center and splits the south pole between the four corners of the square, forming a quincunx pattern that resembles the “five” marking on a standard six-sided die. This arrangement has been previously used by the Peirce quincuncial projection, the Collignon quincuncial projection, and the Gringorten projection.¹

The development of the projection was motivated as a method to store spherical panoramic images, for potential use as a new format for the Pannellum panorama viewer. Since GPU texture limits are defined in terms of square textures, a square projection is ideal for such a use, and a quincuncial arrangement will in general have lower distortion than something like a cylindrical projection, since the sphere is cut in more places. A quincuncial arrangement is also seamlessly tileable, which can help to avoid sampling issues at the image edges. Additionally, to avoid wasting pixels due to varying levels of spatial detail, an equal-area projection is preferred, eliminating the Peirce quincuncial projection from contention, since it is a conformal projection.² For existing projections, this left the Collignon quincuncial projection and the Gringorten projection. However, the Gringorten projection does not have closed-form solutions, which prevents its use in a GPU shader. This left just the Collignon quincuncial projection, but it has significant angular distortion and cusps, which will increase visual artifacts in the projected panorama view and will likely decrease the effectiveness of lossy image compression, e.g., JPEG compression. Thus, the goal was to develop a new projection that had relatively low angular distortion like the Gringorten projection but had closed-form solutions, allowing for a GPU shader implementation.

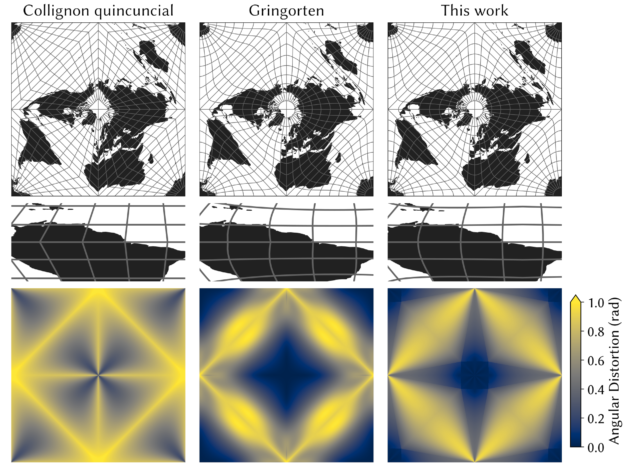
After going through many, many pages of scratch paper, I developed the new projection described in the paper, which met the design goals. It has closed-form solutions and has comparable—although slightly higher—average angular distortion to that of the Gringorten projection. However, it has lower maximum angular distortion and has only almost-imperceptible cusps. As it does not have a large, arguably-unsightly cusp along the equator like the Gringorten projection, it is probably a better projection even for cartographic purposes, where the lack of closed-form solutions does not present an issue. A comparison of the new projection with the Collignon quincuncial projection and the Gringorten projection is shown below.

The paper’s supplementary information contains all the code necessary to reproduce the paper’s figures, including a Python implementation of the projection and a D3.js implementation. Before including the projection in Pannellum, a detailed comparison of the new projection to existing cube-based equal-area and near-equal-area projections needs to be completed.

1. Gringorten, Irving I. “A square equal-area map of the world.” Journal of Applied Meteorology and Climatology 11, no. 5 (1972): 763–767.  ↩

2. A projection cannot be simultaneously conformal (angle preserving) and equal area.  ↩